Solving Most Systems of Random Quadratic Equations
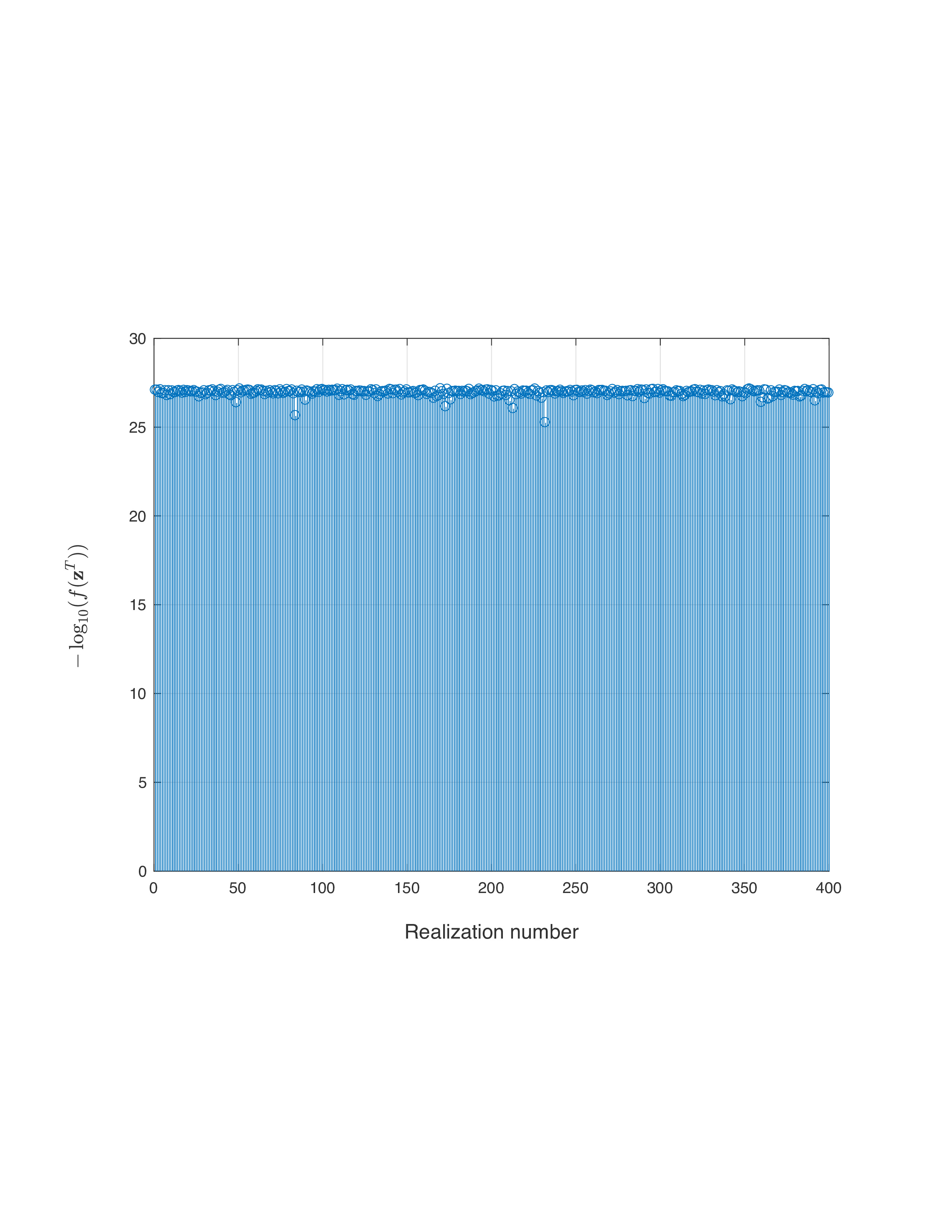 |
To show the power of RAF in the high-dimensional regime, the amplitude-based least-squares loss function value |
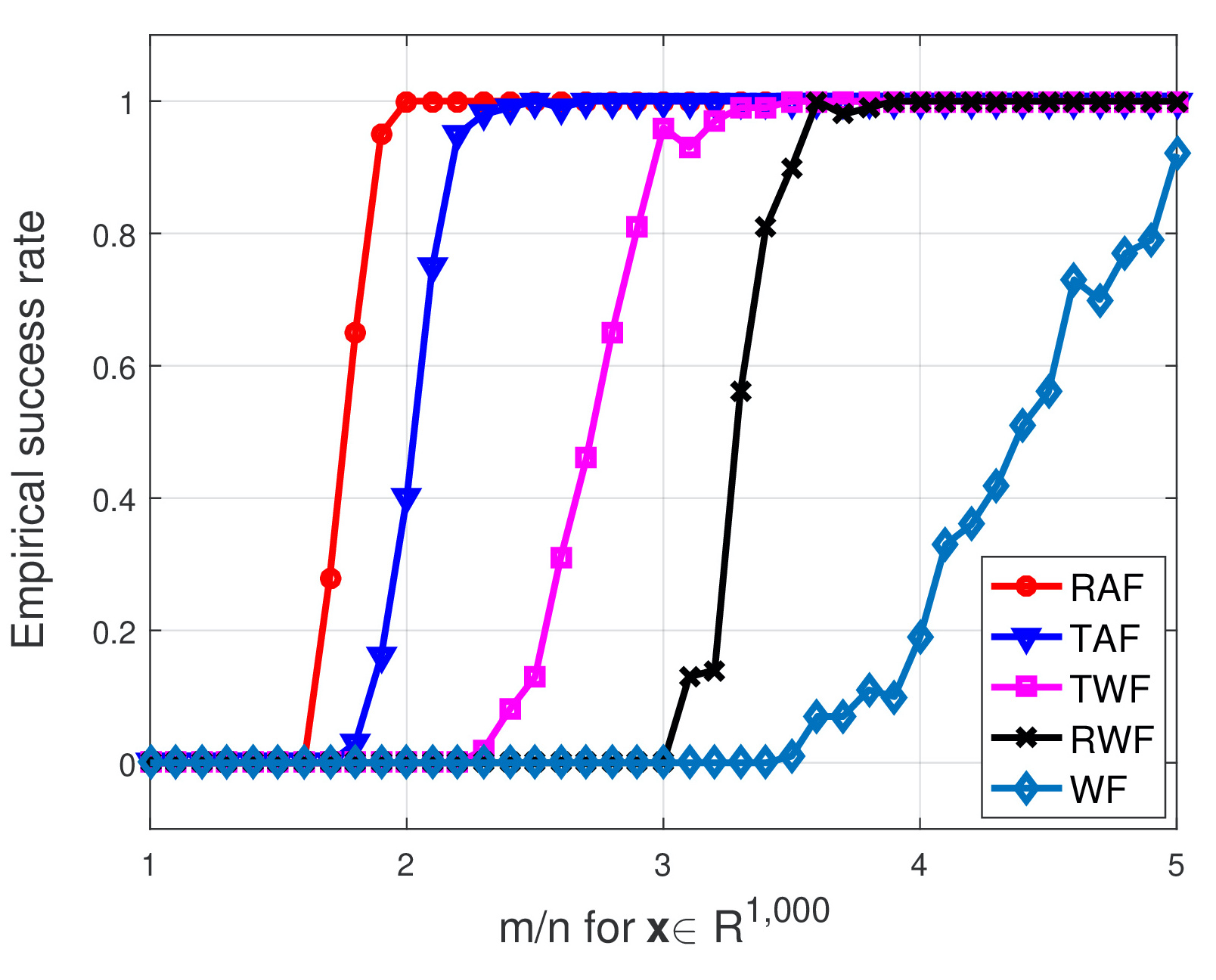 |
The left figure compares the empirical success rate of five schemes
with the signal dimension being fixed at |
Solving Most Systems of Random Quadratic Equations (Preprint),(Poster)
Authors: G. Wang, G. B. Giannakis, Y. Saad, and J. Chen
This paper deals with finding an 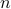 -dimensional solution
-dimensional solution 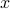 to a system of quadratic equations of the form
to a system of quadratic equations of the form 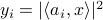 for
for 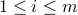 , which is also known as phase retrieval and is NP-hard in general. We put forth a novel procedure for minimizing the amplitude-based least-squares empirical loss, that starts with a weighted maximal correlation initialization obtainable with a few power or Lanczos iterations, followed by successive refinements based upon a sequence of iteratively reweighted (generalized) gradient iterations. The two (both the initialization and gradient flow) stages distinguish themselves from prior contributions by the inclusion of a fresh (re)weighting regularization technique. The overall algorithm is conceptually simple, numerically scalable, and easy-to-implement. For certain random measurement models, the novel procedure is shown capable of finding the true solution
, which is also known as phase retrieval and is NP-hard in general. We put forth a novel procedure for minimizing the amplitude-based least-squares empirical loss, that starts with a weighted maximal correlation initialization obtainable with a few power or Lanczos iterations, followed by successive refinements based upon a sequence of iteratively reweighted (generalized) gradient iterations. The two (both the initialization and gradient flow) stages distinguish themselves from prior contributions by the inclusion of a fresh (re)weighting regularization technique. The overall algorithm is conceptually simple, numerically scalable, and easy-to-implement. For certain random measurement models, the novel procedure is shown capable of finding the true solution 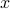 in time proportional to reading the data
in time proportional to reading the data 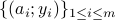 . This holds with high probability and without extra assumption on the signal
. This holds with high probability and without extra assumption on the signal 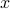 to be recovered, provided that the number
to be recovered, provided that the number 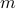 of equations is some constant
of equations is some constant 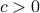 times the number
times the number 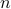 of unknowns in the signal vector, namely,
of unknowns in the signal vector, namely,  . Empirically, the upshots of this contribution are: i) (almost)
. Empirically, the upshots of this contribution are: i) (almost) 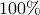 perfect signal recovery in the high-dimensional (say e.g.,
perfect signal recovery in the high-dimensional (say e.g.,  ) regime given only an emph{information-theoretic limit} number of noiseless equations, namely,
) regime given only an emph{information-theoretic limit} number of noiseless equations, namely, 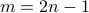 in the real-valued Gaussian case; and, ii) (nearly) optimal statistical accuracy in the presence of additive noise of bounded support. Finally, substantial numerical tests using both synthetic data and real images corroborate markedly improved signal recovery performance and computational efficiency of our novel procedure relative to state-of-the-art approaches.
in the real-valued Gaussian case; and, ii) (nearly) optimal statistical accuracy in the presence of additive noise of bounded support. Finally, substantial numerical tests using both synthetic data and real images corroborate markedly improved signal recovery performance and computational efficiency of our novel procedure relative to state-of-the-art approaches.
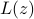 evaluated at the returned estimate
evaluated at the returned estimate 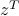 for
for 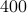 MC realizations is plotted (in negative logarithmic scale) in figure on the left, where the number of simulated noiseless measurements was set to be the information-theoretic limit, namely,
MC realizations is plotted (in negative logarithmic scale) in figure on the left, where the number of simulated noiseless measurements was set to be the information-theoretic limit, namely, 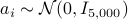 , and
, and 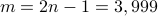 for
for 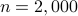 . It is self-evident that our proposed RAF approach returns a solution of function value
. It is self-evident that our proposed RAF approach returns a solution of function value  smaller than
smaller than 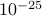 in all
in all 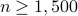 ) signals exactly from an emph{optimal number} of random quadratic equations, which also provides a positive answer to the question posed easier in the Introduction.
) signals exactly from an emph{optimal number} of random quadratic equations, which also provides a positive answer to the question posed easier in the Introduction.  while the ratio
while the ratio
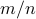 increasing by
increasing by 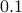 from
from  to
to 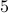 . As clearly depicted by the plots, our RAF (the red plot) enjoys markedly improved performance over its competing alternatives. Moreover, it also achieves
. As clearly depicted by the plots, our RAF (the red plot) enjoys markedly improved performance over its competing alternatives. Moreover, it also achieves 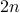 , where the others do not work (well).
, where the others do not work (well).