 |
Given observed data Besides linear sample complexity
|
Solving Large-scale Systems of Random Quadratic Equations via Stochastic Truncated Amplitude Flow.
Authors: G. Wang, G. B. Giannakis, and J. Chen
This paper develops a new algorithm, which we call
emph{stochastic truncated amplitude flow} (STAF), to reconstruct an unknown  -dimensional (typically
-dimensional (typically  very large) signal
very large) signal 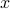 from
from 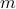 phaseless quadratic equations of the form
phaseless quadratic equations of the form 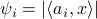 .
This problem, also known as phase retrieval, is emph{NP-hard} in general.
Adopting an amplitude-based nonconvex formulation, STAF is an iterative solution algorithm comprising two stages: s1) The first stage employs a stochastic variance reduced gradient algorithm to solve for an orthogonality-promoting initialization; and, s2) the second stage iteratively refines the initialization using stochastic truncated amplitude-based gradient iterations. Both stages process a single equation per iteration, thus rendering STAF a simple, scalable, and fast algorithm amenable to large-scale implementations.
Under the Gaussian random
.
This problem, also known as phase retrieval, is emph{NP-hard} in general.
Adopting an amplitude-based nonconvex formulation, STAF is an iterative solution algorithm comprising two stages: s1) The first stage employs a stochastic variance reduced gradient algorithm to solve for an orthogonality-promoting initialization; and, s2) the second stage iteratively refines the initialization using stochastic truncated amplitude-based gradient iterations. Both stages process a single equation per iteration, thus rendering STAF a simple, scalable, and fast algorithm amenable to large-scale implementations.
Under the Gaussian random 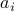 designs, we prove that STAF recovers exactly any signal
designs, we prove that STAF recovers exactly any signal 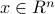 exponentially fast from on the order of
exponentially fast from on the order of  quadratic equations.
STAF is also robust vis-{`a}-vis additive noise of bounded support.
Simulated tests using the real Gaussian
quadratic equations.
STAF is also robust vis-{`a}-vis additive noise of bounded support.
Simulated tests using the real Gaussian 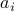 designs
demonstrate that STAF empirically reconstructs any
designs
demonstrate that STAF empirically reconstructs any 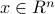 exactly from about
exactly from about 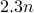 magnitude-only measurements, outperforming the-state-of-arts and narrowing the gap from the information-theoretic number of quadratic equations
magnitude-only measurements, outperforming the-state-of-arts and narrowing the gap from the information-theoretic number of quadratic equations  . Extensive experiments using synthetic data and real images corroborate markedly improved performance of STAF over existing alternatives.
. Extensive experiments using synthetic data and real images corroborate markedly improved performance of STAF over existing alternatives.
 and feature vectors
and feature vectors 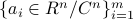 , our goal is to solve for
, our goal is to solve for 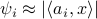 ,
, 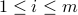 .
.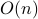 and computational complexity
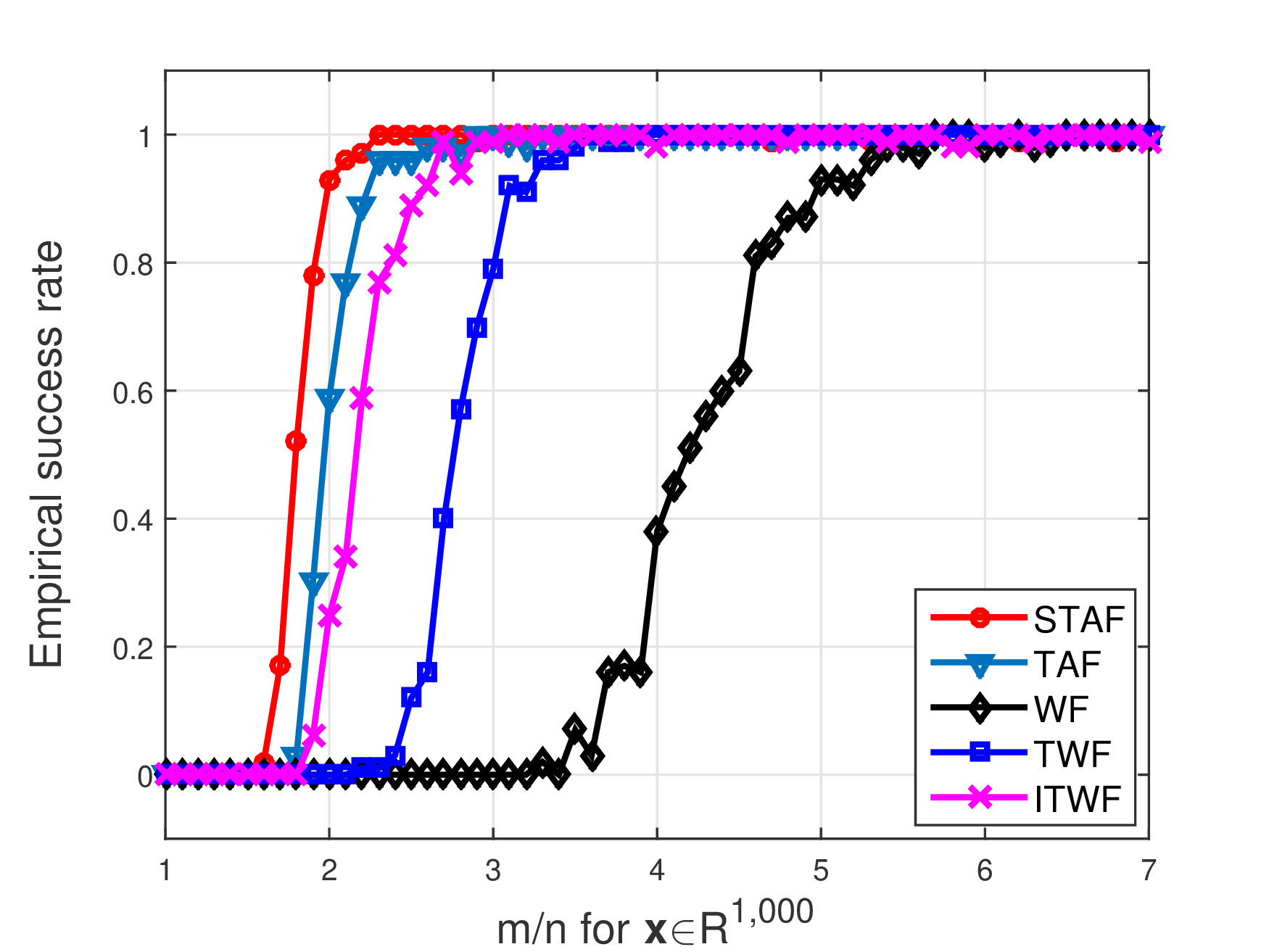
and computational complexity  , our Stochastic Truncated Amplitude Flow (STAF) performs only stochastic iterations achieving the optimal-order iteration complexity amenable to large-scale imaging applications.
, our Stochastic Truncated Amplitude Flow (STAF) performs only stochastic iterations achieving the optimal-order iteration complexity amenable to large-scale imaging applications.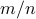 is about 2.3; this is in sharp contrast with 3 for TAF, 4.5 for TWF, and 7 for WF.
is about 2.3; this is in sharp contrast with 3 for TAF, 4.5 for TWF, and 7 for WF.