Solving Systems of Random Quadratic Equations via Truncated Amplitude Flow
Our method adopts the amplitude-based cost function and proceeds in two stages: In stage one, we introduce an orthogonality-promoting initialization that is obtained with a few simple power iterations. Stage two refines the initial estimate by successive updates of scalable truncated generalized gradient iterations.
Orthogonality-promoting initialization
Leveraging the Strong Law of Large Numbers (SLLN), spectral initialization methods estimate  as the (appropriately scaled) leading eigenvector of
as the (appropriately scaled) leading eigenvector of 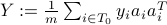 , where
, where 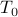 is an index set accounting for possible data truncation. As asserted in TWF paper, each summand
is an index set accounting for possible data truncation. As asserted in TWF paper, each summand  follows a heavy-tail probability density function lacking a moment generating function. This causes major performance degradation especially when the number of measurements is small. Instead of spectral initializations, we shall take another route to bypass this hurdle. To gain intuition for our initialization,
a motivating example is presented first that reveals fundamental characteristics of high-dimensional random vectors.
follows a heavy-tail probability density function lacking a moment generating function. This causes major performance degradation especially when the number of measurements is small. Instead of spectral initializations, we shall take another route to bypass this hurdle. To gain intuition for our initialization,
a motivating example is presented first that reveals fundamental characteristics of high-dimensional random vectors.
 |
A curious experiment: Fixing any nonzero vector 
where |
This example corroborates the folklore that random vectors in high-dimensional spaces are almost always nearly orthogonal to each other.
This inspired us to pursue an orthogonality-promoting initialization method. Our key idea is to approximate 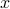 by a vector that is most orthogonal to a subset of vectors
by a vector that is most orthogonal to a subset of vectors 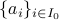 , where
, where  is an index set with cardinality
is an index set with cardinality  that includes indices of the smallest
squared normalized
inner-products
that includes indices of the smallest
squared normalized
inner-products 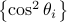 .
.
Truncated amplitude based gradient iterations
Precisely, if 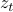 and
and 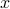 lie in different sides of the hyperplane
lie in different sides of the hyperplane 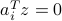 , then the sign of
, then the sign of  will be different than that of
will be different than that of 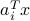 ; that is,
; that is, 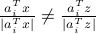 . Specifically, one can re-write the
. Specifically, one can re-write the  -th generalized gradient component as
-th generalized gradient component as
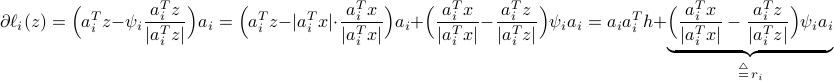
where 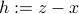 .
Intuitively, the SLLN asserts that averaging the first term
.
Intuitively, the SLLN asserts that averaging the first term 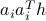 over
over 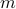 instances approaches
instances approaches  , which qualifies it as a desirable search direction. However,
certain generalized gradient entries involve erroneously estimated signs of
, which qualifies it as a desirable search direction. However,
certain generalized gradient entries involve erroneously estimated signs of 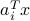 ; hence, nonzero
; hence, nonzero 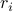 terms exert a negative influence on the search direction
terms exert a negative influence on the search direction  by dragging the iterate away from
by dragging the iterate away from 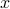 , and they typically have sizable magnitudes.
, and they typically have sizable magnitudes.
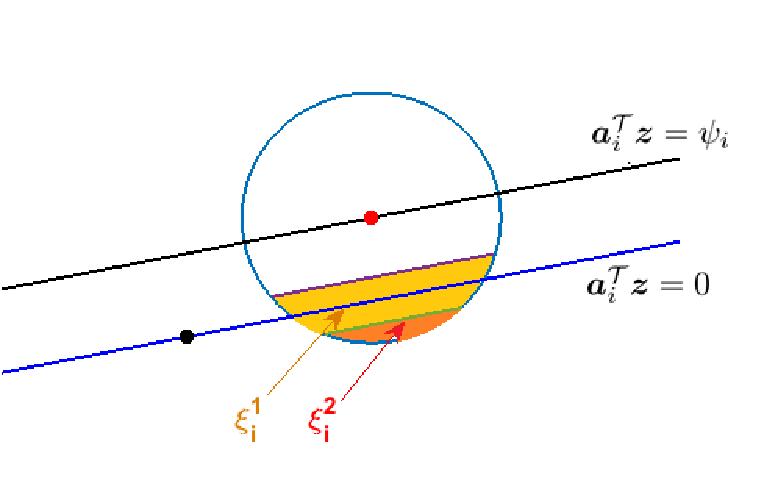 |
The geometric understanding of the proposed truncation rule on the |
Nevertheless, it is difficult or even impossible to check whether the sign of  equals that of
equals that of 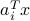 . Fortunately, as demonstrated in Fig. ref{fig:truncation},
most spurious generalized
gradient components (those corrupted by nonzero
. Fortunately, as demonstrated in Fig. ref{fig:truncation},
most spurious generalized
gradient components (those corrupted by nonzero 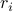 terms) hover around the watershed hyperplane
terms) hover around the watershed hyperplane 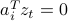 . For this reason, TAF includes only those components
having
. For this reason, TAF includes only those components
having 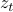 sufficiently away from its watershed, i.e.,
vspace{-.em}
sufficiently away from its watershed, i.e.,
vspace{-.em}
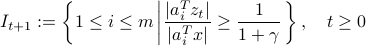
for an appropriately selected threshold 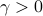 . To be more specific, the light yellow color-coded area denoted by
. To be more specific, the light yellow color-coded area denoted by 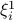 in Figure above
signifies the truncation region of
in Figure above
signifies the truncation region of  , i.e.,
if
, i.e.,
if  obeying the condition above, the corresponding generalized gradient component
obeying the condition above, the corresponding generalized gradient component 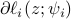 will be thrown out. However, the truncation rule may mis-reject the ‘good’ gradients if
will be thrown out. However, the truncation rule may mis-reject the ‘good’ gradients if 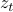 lies in the upper part of
lies in the upper part of 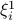 ; and ‘bad’ gradients may be missed as well if
; and ‘bad’ gradients may be missed as well if 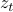 belongs to the spherical cap
belongs to the spherical cap 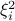 .
Fortunately,
the probabilities of the miss and the mis-rejection are provably very small, hence precluding a noticeable influence on the descent direction. Although not perfect, it turns out that
such a regularization rule succeeds in detecting and eliminating most corrupted generalized gradient components and hence maintaining a well-behaved search direction.
.
Fortunately,
the probabilities of the miss and the mis-rejection are provably very small, hence precluding a noticeable influence on the descent direction. Although not perfect, it turns out that
such a regularization rule succeeds in detecting and eliminating most corrupted generalized gradient components and hence maintaining a well-behaved search direction.
 |
 |
 |
The recovered Milky Way Galaxy images after i) truncated spectral initialization (top); ii) orthogonality-promoting initialization (middle); and iii) 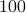 TAF gradient iterations refining the orthogonality-promoting initialization (bottom), where
TAF gradient iterations refining the orthogonality-promoting initialization (bottom), where 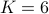 masks were employed in our experiment. Specifically, the algorithm was run independently on each of the three bands. A number
masks were employed in our experiment. Specifically, the algorithm was run independently on each of the three bands. A number 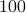 of power iterations were used to obtain an initialization, which was refined by
of power iterations were used to obtain an initialization, which was refined by 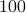 gradient-type iterations. The relative errors after our orthogonality-promoting initialization and after
gradient-type iterations. The relative errors after our orthogonality-promoting initialization and after 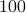 TAF iterations are
TAF iterations are 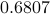 and
and 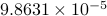 , respectively. In sharp contrast, TWF returns images of corresponding relative errors
, respectively. In sharp contrast, TWF returns images of corresponding relative errors 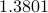 and
and 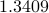 , which are far away from the ground truth.
, which are far away from the ground truth.
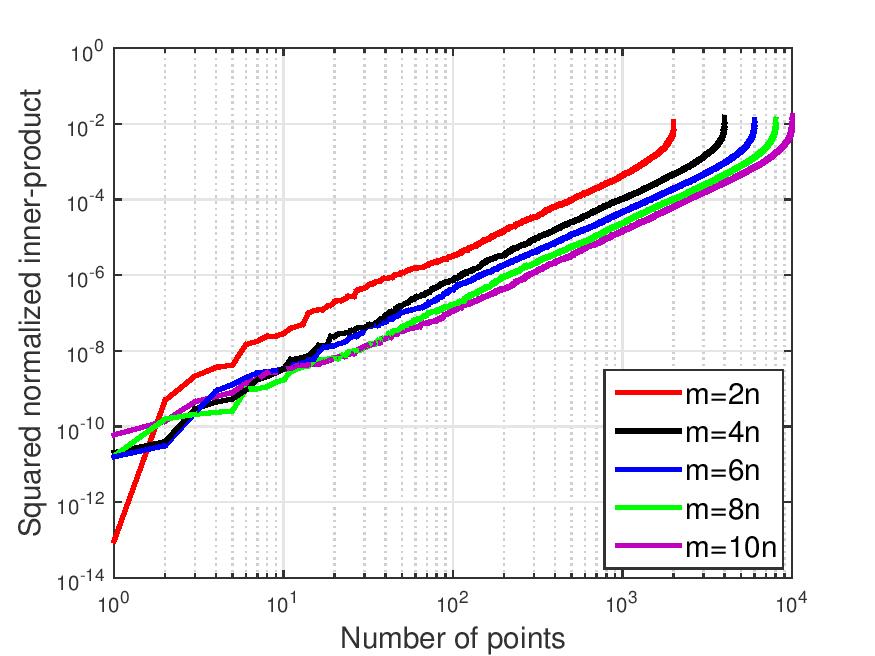
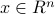 , generate data
, generate data 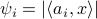 using i.i.d.
using i.i.d. 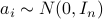 ,
, 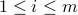 . Then evaluate the following squared normalized inner-product
. Then evaluate the following squared normalized inner-product 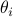 is the angle between vectors
is the angle between vectors 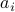 and
and 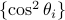 in an ascending fashion, and collectively
denote them as
in an ascending fashion, and collectively
denote them as ![{xi}:=[cos^2theta_{[m]}~cdots~cos^2theta_{[1]}]^T](eqs/7148505495767972956-130.png) with
with
![cos^2theta_{[1]} %gecos^2theta_{[2]} gecdotsgecos^2theta_{[m]}](eqs/1226858015667637714-130.png) . Figure ref{fig:inner} plots the ordered entries in
. Figure ref{fig:inner} plots the ordered entries in 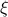 for
for 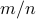 varying by
varying by 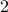 from
from  %
%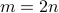 ,
, 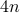 ,
, 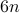 ,
, 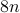 , and
, and 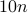 with
with 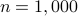 . Observe that almost all
. Observe that almost all
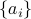 vectors have a squared normalized inner-product with
vectors have a squared normalized inner-product with 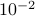 , while half of the inner-products are less than
, while half of the inner-products are less than  , which implies that
, which implies that  , where the red dot denotes the solution
, where the red dot denotes the solution 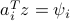 and
and 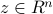 ) passing through points
) passing through points 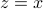 and
and  , respectively, are shown.
, respectively, are shown.